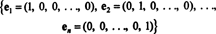Applications of Derivatives

Study about the applications of derivatives,
Let us began this chapter with the following statement:

* Often a physician may want to test how small changes in dosage can affect the body's response to a particular drug.

* An economist may want to study how investment changes with variation in interest rates.

* How the velocity of a heavy meteorite entering the earth's surface, changes with the its distance from the earth's surface.

* For a given volume of oil, what is the least expensive shape of an oil can?

These questions and many, more such practical problems can be expressed and solved by applying derivative.

Differential calculus can be considered as mathematics of motion, growth and change where there is a motion, growth, change. Whenever there is variable forces producing acceleration, differential calculus is the right mathematics to apply. Application of derivatives are used to represent and interprete the rate at which quantities change with respect to another variable. Most of the changes are considered in terms of independent variable time. But there is no restriction that the changes are considered with respect to time only, as we have seen in the above mentioned, statements.
I hope the above explanation was useful, now let me explain Trigonometric Equations.

Introduction of Cartesian coordinate system

Let us study about cartesian coordinate system,
The Cartesian coordinate system was developed by the mathematician Descartes during an illness. As he lay in bed sick, he saw a fly buzzing around on the ceiling, which was made of square shaped tiles. As he watched he realized that he could describe the position of the fly by the ceiling tile he was on. After this experience he developed the coordinate plane to make it easier to describe the position of objects.

one of the coordinates in a system of coordinates that locates a point on a plane or in space by its distance from two lines or three planes respectively; the two lines or the intersections of the three planes are the coordinate axes.

I hope the above explanation was useful.

A Basis for a Vector Space

Let V be a subspace of R ⁿ for some n. A collection B = { v₁, v₂, …, v _r } of vectors from V is said to be a basis for V if B is linearly independent and spans V. If either one of these criterial is not satisfied, then the collection is not a basis for V. If a collection of vectors spans V, then it contains enough vectors so that every vector in V can be written as a linear combination of those in the collection. If the collection is linearly independent, then it doesn't contain so many vectors that some become dependent on the others. Intuitively, then, a basis has just the right size: It's big enough to span the space but not so big as to be dependent.

Example 1: The collection { i, j} is a basis for R², since it spans R² and the vectors i and j are linearly independent (because neither is a multiple of the other). This is called the standard basis for R². Similarly, the set { i, j, k} is called the standard basis for R³, and, in general,
is the standard basis for R ⁿ.

I hope the above explanation was useful.

Probability of Joint Occurrences

Let us study about
Probability of Joint Occurrences :

Another way to compute the probability of all three flipped coins landing heads is as a series of three different events: first flip the penny, then flip the nickel, then flip the dime. Will the probability of landing three heads still be .125?

Multiplication rule :

To compute the probability of two or more independent events all occurring— joint occurrence—multiply their probabilities.

For example, the probability of the penny landing heads is 1/2, or .5; the probability of the nickel next landing heads is 1/2, or .5; and the probability of the dime landing heads is 1/2, or .5; thus, note that

.5 x .5 x .5 = .125

which is what you determined with the classic theory by assessing the ratio of number of favorable outcomes to number of total outcomes. The notation for joint occurrence is P(AB) = P(A) × P(B) and reads: The probability of A and B both happening is equal to the probability of A times the probability of B.

Using the multiplication rule, you can also determine the probability of drawing two aces in a row from a deck of cards. The only way to draw two aces in a row from a deck of cards is for both draws to be favorable. For the first draw, the probability of a favorable outcome is 4/52. But because the first draw is favorable, only 3 aces are left among 51 cards. So the probability of a favorable outcome on the second draw is 3/51. For both events to happen, you simply multiply those two probabilities together:
Note that these probabilities are not independent. If, however, you had decided to return the initial card drawn back to the deck before the second draw, then the probability of drawing an ace on each draw is 4/52, as these events are now independent. Drawing an ace twice in a row, with the odds being 4/52 both times, gives the following:

In either case, you use the multiplication rule because you are computing probability for favorable outcomes in all events.
Hope the above information was helpful.

Definitions of the Determinant

Definitions of the Determinant :

The determinant function can be defined by essentially two different methods. The advantage of the first definition—one which uses permutations—is that it provides an actual formula for det A, a fact of theoretical importance. The disadvantage is that, quite frankly, no one actually computes a determinant by this method.

Method 1 for defining the determinant. If n is a positive integer, then a permutation of the set S = {1, 2, …, n} is defined to be a bijective function—that is, a one-to-one correspondence—σ, from S to S. For example, let S = {1, 2, 3} and define a permutation σ of S as follows:
Since σ(1) = 3, σ(2) = 1, and σ(3) = 2, the permutation σ maps the elements 1, 2, 3 into 3, 1, 2. Intuitively, then, a permutation of the set S = {1, 2, …, n} provides a rearrangement of the numbers 1, 2, …, n. Another permutation, σ′, of the set S is defined as follows:
This permutation maps the elements 1, 2, 3 into 2, 1, 3, respectively. This result is written
Hope the above explanation was useful, not let me explain you about adjoint matrix.

Rhombus

Rhombus:

Introduction to Rhombus:

Let us learn about the properties of a Rhombus,its shape and also other basic features of a Rhombus.

Rhombus is quadrilaterals with both pairs of opposite sides are parallel and all the sides are having same length. Rhombus is also called as equilateral parallelogram.

The rhombus is also called as diamond and rhomb. A square is also a rhombus, because the square is a quadrilateral with all sides equal.

All the opposite sides of the rhombus is parallel and all the opposite angles are equal.

Properties of Rhombus:

• Opposite angles of the rhombus having equal measures.

• The diagonals of the rhombus intersect each other at right angles.

• Rhombus having two diagonals that are connecting opposite pairs of vertices.

• Rhombus is Symmetric along the diagonals

• Every Rhombus is parallelogram

• All the parallelograms are not a Rhombus

• Dual polygon of the rhombus is called as Rectangle.

Area and Perimeter of Rhombus:

Area of the Rhombus:

The area of the Rhombus is same as the area of the parallelogram .That is the area is the multiplication of base and height.

The formula for calculate the area is,

A=b * h

The base of the rhombus is the length of one of its sides and the height is the perpendicular distance between the opposite sides.

Perimeter of the Rhombus:

The perimeter of the rhombus is the total sum of its all the sides length. Generally the perimeter is sum of the length of the all sides. In the case of rhombus, all the sides are having equal length. So we can say that the perimeter is 4s, where s is length of the sides.

Altitude of the rhombus:

The perpendicular distance between the opposite side and the base of a rhombus is called as Altitude of the rhombus. The altitude also mentioned as the height.

Angles of a rhombus:

Sum of the adjacent sides of any rhombus are equal to 180 degree. That is adjacent angles of a rhombus are supplementary.

Hope you like the above example of Rhombus.Please leave your comments, if you have any doubts.

Cone:

When we talk about a cone the first thing that comes to our mind is an ice-cream,I'am sure we have all seen an ice-cream cone,now let us learn about the shape of a cone in the mathematical sense.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat, usually circular base to a point called the apex or vertex.

Cylinder:

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given straight line, the axis of the cylinder.In this article we shall see how to calculate volume of cone and cylinder.Now that we have understood the meaning of cone and sphere let us look at the other aspects of this topic,basically now we will learn about the volume of a cone and sphere.

Volume of Cone:

Formula for volume of the cone (v) =1/3 π r2 h cubic units

V=volume of cone

r=radius

h=height

Example problems:

1. The cone has the radius = 3 cm and height = 7 cm. Find the volume of the cone.

Solution:

Given:

Radius (r) = 3 cm

Height (h) =7 cm

Formula:

The volume of the cone =1/3 x π x r2 x h cubic units

= 1/3 x 3.14 x (3)2 x 7

= 65.94

The volume of the cone = 65.94 cm3

2. The cone has the radius = 8 cm and height = 14 cm. Find the volume of the cone.

Solution:

Given:

Radius (r) = 8 cm

Height (h) = 14 cm

Formula:

The volume of the cone =1/3 x π x r2 x h cubic units

= 1/3 x 3.14 x (8)2 x 14

= 937.81

The volume of the cone = 937.81 cm3

Volume of Cylinder:

cylinder

Formula for volume of the cylinder (v) = π r2 h cubic units

V=volume of cylinder

r=radius

h=height

1. The cylinder has the radius r= 3 cm, h= 11 cm. Find the volume of cylinder.

Solution:

Given:

r=3 cm

h=11 cm

Formula:

The volume of the cylinder = π x r2 x h cubic unit

=3.14 x (3)2 x 11

= 310.86

The volume of the cylinder = 310.86 cm3



2. The cylinder has the radius r= 8 cm, h=13 cm. Find the volume of cylinder.

Solution:

Given:

r=8 cm

h=13 cm

Formula:

The volume of the cylinder = π x r2 x h cubic unit

=3.14 x (8)2 x 13

= 2612.48

The volume of the cylinder = 2612.48 cm3

Hope you like the above example of Cone and Cylinder.Please leave your comments, if you have any doubts.