The determinant function can be defined by essentially two different methods. The advantage of the first definition—one which uses permutations—is that it provides an actual formula for det A, a fact of theoretical importance. The disadvantage is that, quite frankly, no one actually computes a determinant by this method.
Method 1 for defining the determinant. If n is a positive integer, then a permutation of the set S = {1, 2, …, n} is defined to be a bijective function—that is, a one-to-one correspondence—σ, from S to S. For example, let S = {1, 2, 3} and define a permutation σ of S as follows:
 Since σ(1) = 3, σ(2) = 1, and σ(3) = 2, the permutation σ maps the elements 1, 2, 3 into 3, 1, 2. Intuitively, then, a permutation of the set S = {1, 2, …, n} provides a rearrangement of the numbers 1, 2, …, n. Another permutation, σ′, of the set S is defined as follows:
Since σ(1) = 3, σ(2) = 1, and σ(3) = 2, the permutation σ maps the elements 1, 2, 3 into 3, 1, 2. Intuitively, then, a permutation of the set S = {1, 2, …, n} provides a rearrangement of the numbers 1, 2, …, n. Another permutation, σ′, of the set S is defined as follows: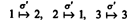 This permutation maps the elements 1, 2, 3 into 2, 1, 3, respectively. This result is written
This permutation maps the elements 1, 2, 3 into 2, 1, 3, respectively. This result is written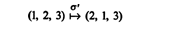 Hope the above explanation was useful, not let me explain you about adjoint matrix.
Hope the above explanation was useful, not let me explain you about adjoint matrix.